|
| C++ 實習測試: 功能簡化的二元搜尋樹
Binary Search Tree 類別製作 |
| 時間: 50分鐘 (10:10 上傳時間截止) |
|
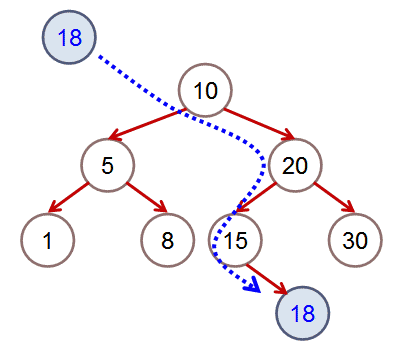
| 下圖是一個功能簡化的 二元搜尋樹
(Binary Search Tree)
概念上
- 一個二元搜尋樹中, 每一個節點左邊子節點的鍵值 小於 此節點的鍵值,
右邊子節點的鍵值 大於或等於
此節點的鍵值
- 下圖中 將鍵值 18 的節點放入二元搜尋樹中, 因為 18 ≥ 10 且 18 <
20 且 18 ≥ 15, 所以 18 會成為 15 的右子節點
- 我們對這個二元搜尋樹定義 insert_node() 函式來提供新增一個節點的功能
- 二元搜尋樹最重要的機制當然是搜尋, 我們定義 find_node() 函式, 傳入一個鍵值,
如果找到了就會傳回那個節點的指標, 如果沒有找到會回傳 0
- 我們再定義一個中序走訪 (inorder traverse) 每一節點並且列印鍵值的函式 print_inorder(),
可以將整個二元搜尋樹的每一個節點以中序印出
- 下面的程式沒有實作 刪除節點 的功能
|
|
|
下面是一個實作這個簡化的 二元搜尋樹 Binary Search Tree
的 C 程式
|
#include <cstdio> // printf()
#include <cstdlib> // malloc(),free(), system()
#include <cassert> // assert()
struct binary_search_tree_node
{
int data;
struct binary_search_tree_node *left;
struct binary_search_tree_node *right;
};
typedef struct binary_search_tree_node BSTNode;
void print_inorder(BSTNode *ptr);
BSTNode *insert_node(BSTNode *root, int value);
BSTNode *find_node(BSTNode *ptr, int value);
int main()
{
int data[] = {10, 20, 5, 8, 30, 15, 1, 18};
int ndata = sizeof(data)/sizeof(int);
BSTNode *head = 0;
for (int i=0; i<ndata; i++)
head = insert_node(head, data[i]);
printf("In order listing: ");
print_inorder(head);
printf("\n"); fflush(stdout);
assert(find_node(head, 15));
assert(!find_node(head, 11));
system("pause");
return 0;
}
// 中序走訪
void print_inorder(BSTNode *ptr)
{
if (ptr != 0)
{
print_inorder(ptr->left); // 走左子樹
printf("%2d ", ptr->data); // 印出節點內容
print_inorder(ptr->right); // 走右子樹
}
}
// 插入節點
BSTNode *insert_node(BSTNode *root, int value)
{
BSTNode *new_node;
BSTNode *current;
BSTNode *parent;
// 建立節點
new_node = (BSTNode *) malloc(sizeof(BSTNode));
new_node->data = value;
new_node->left = 0;
new_node->right = 0;
if (root == 0) // 目前無資料
{
return new_node;
}
else
{
current = root; // 從頭找要新節點之插入點
while (current != 0)
{
parent = current; // 找新節點之父節點
if (current->data > value)
current = current->left; // 往左找
else
current = current->right; // 往右找
}
if (parent->data > value) // 插入此父節點左邊或右邊
parent->left = new_node;
else
parent->right = new_node;
}
return root; // 回傳此樹
}
// 尋找節點
BSTNode *find_node(BSTNode *ptr, int value)
{
// 從 ptr 指到的節點開始找
while (ptr != 0)
{
if (___________ == ___________) // 如果找到目標
return ptr; // 回傳此節點位址
else if (___________ > ___________) // 如果目前節點的鍵值比 value 大
__________ // 向左邊子節點移動
else
__________ // 向右邊子節點移動
}
return 0; // 找不到
} |
| 時間: 50分鐘 (10:10
上傳時間截止)
請在 Visual Studio 中製作一個新方案, 加入一個 C_Version 的專案
- 拷貝上述程式到 main.cpp, 完成上面的 find_node() 函式的功能, 並且測試
[在完成 find_node() 的功能之前, 你還是可以先把 main() 裡面相關的測試註解掉來編譯, 確定你的專案沒有錯誤]
請再上述方案中加入一個新的 CPP_Version 專案
- 請加入一個 main.cpp 測試程式,其內容主體由上面的 main() 函式修改為
int main()
{
int data[] = {10, 20, 5, 8, 30, 15, 1, 18};
int ndata = sizeof(data)/sizeof(int);
BinarySearchTree bst;
bst.initialize();
for (int i=0; i<ndata; i++)
bst.insert(data[i]);
printf("In order listing: ");
bst.print_inorder();
printf("\n"); fflush(stdout);
assert(bst.find(15));
assert(!bst.find(11));
system("pause");
return 0;
}
請注意:
1. 上面程式片段並沒有包含需要引入的函式庫宣告
2. BinarySearchTree 類別的界面已經運用封裝的概念稍作修改, BinarySearchTree 以外的程式不需要看到
BSTNode 這種結構, BinarySearchTree 的使用方法也已經改為物件化的訊息傳遞
- 請配合上面的 main() 測試函式, 製作一個 BinarySearchTree 類別
- 類別裡有一個資料成員 m_root 指向搜尋樹的樹根
- 類別裡需要有四個成員函式:
void initialize()
void insert(int)
void print_inorder()
bool find(int)
請由範例 C 程式中三個函式 print_inorder, insert_node, find_node 修改出 print_inorder,
insert, find 三個成員函式, initialize 函式則請初始化資料成員 m_root
請注意: 要在類別中實作一個遞迴的演算法, 函式必須要有參數, 上面的 print_inorder() 介面是沒有參數的, 所以需要另外定義一個私有的成員函式
void print_inorder(BSTNode *ptr) 來完成, print_inorder() 函式裡則呼叫 print_inorder(m_root)
即可
- 請測試, 確保功能正確
|
| 將所完成的程式方案 (只需保留 .cpp, .h, .sln 以及 .vcxproj 檔案即可; 刪除掉
.suo, .sdf, .filters, .users, debug\ 資料匣, 以及 ipch\ 資料匣下的所有內容) 以
zip/rar/7zip 程式將整個資料匣壓縮起來, 在作業區選擇 Labtest1上傳 |
| 範例程式碼
完整操作過程
(android com.adobe.flashplayer.apk)
|
後續你自己可加強之工作
- 這個程式有記憶體的問題, 請運用 memory_leak.h
和 memory_leak.cpp,
在你的專案裡確定這個錯誤
- 請再加入一個成員函式 freeMem() 來釋放整個二元搜尋樹, 並且確定前面的錯誤已經消除
- 目前使用 malloc()/free() 來配置記憶體, 可以練習換成 new/delete
- 目前使用 cstdio 輸出入函式庫, 可以練習換成物件化的 iostream 輸出入函式庫
- struct BSTNode 可以設計成一個 BinarySearchTree 類別私有的的內部結構
- 這個 BinarySearchTree 目前沒有刪除指定節點
remove() 的功能, 可以練習撰寫, 下面是 C 版本的 delete_node() 函式,
刪除一個節點以後, 函式回傳根節點的的指標 (如果原來的根節點被刪除才不致於遺失整個二元搜尋樹), 如果在二元搜尋樹中沒有找到指定節點的話,
delete_node() 沒有回報任何訊息
BSTNode *find_parent(BSTNode *ptr, int value, int *pos)
{
BSTNode *parent;
parent = ptr; // 從ptr開始找
*pos = 0;
while (ptr != 0)
{
if (ptr->data == value) // 找到目標
return parent; // 回傳此節點之父節點
else
{
parent = ptr;
if (ptr->data > value)
{
*pos = -1; // ptr在parent左子樹
ptr = ptr->left; // 往左找
}
else
{
*pos = 1; // ptr在parent右子樹
ptr = ptr->right;// 往右找
}
}
}
return 0; // 找不到
}
// 刪除節點
BSTNode *delete_node(BSTNode *root, int value)
{
BSTNode *parent;
BSTNode *ptr;
BSTNode *next;
int pos;
parent = find_parent(root, value, &pos); // 從root開始,找value之父節點
if (parent != NULL) // 有找到, 準備刪除
{
switch(pos) // 判斷目前節點在父節點左邊或右邊
{
case -1:
ptr = parent->left;
break;
case 1:
ptr = parent->right;
break;
case 0:
ptr = parent;
break;
}
if (ptr->left == 0) // 情況1: 節點沒有左子樹
{
if (parent == ptr) // 如果要刪的是根節點
root = root->right;
else // 其他
{
if (pos == 1)
{
//要刪除的節點在父節點右方,所以將父節點的右節點指向刪除節點的右節點
parent->right = ptr->right;
}
else
{
//要刪除的節點在父節點左方,所以將父節點的左節點指向刪除節點的右節點
parent->left = ptr->right;
}
}
free(ptr);
}
else if (ptr->right == 0) // 情況2: 節點沒有右子樹
{
if (parent == ptr) // 如果要刪的是根節點
root = root->left;
else
{
if (pos == 1)
{
//要刪除的節點在父節點右方,所以將父節點的右節點指向刪除節點的左節點
parent->right = ptr->left;
}
else
{
//要刪除的節點在父節點左方,所以將父節點的左節點指向刪除節點的左節點
parent->left = ptr->left;
}
}
free(ptr);
}
else // 情況3: 節點有左右子樹
{
parent = ptr;
next = ptr->left; // 找取代點next, 從ptr左邊開始找
while (next->right != 0)// 往左子節點之右子樹找最大值當取代點
{
parent = next; // parent為next之父節點
next = next->right;
}
ptr->data = next->data; // 取代!!
parent->right = next->left; // 繞過next節點
free(next); // 刪除next (注意: 不是刪除ptr)
}
}
return root; // 回傳此樹
}
配合的功能測試程式碼如下
if (find_node(head, 18))
{
head = delete_node(head, 18);
assert(!find_node(head, 18));
}
printf("In order listing: ");
print_inorder(head);
printf("\n"); fflush(stdout);
if (find_node(head, 10))
{
head = delete_node(head, 10);
assert(!find_node(head, 10));
assert(find_node(head, 15));
}
printf("In order listing: ");
print_inorder(head);
printf("\n"); fflush(stdout);
- 可以把 main() 裡面的測試搬到 BinarySearchTree 類別裡作為簡單的單元測試
- 可以加強 自動驗證是否正確的程式碼, 取代目前列印出來用眼睛看的測試
- initialize() 函式的功能應該用建構元 (constructor) 函式取代, freeMem() 函式的功能應該被解構元
(destructor) 函式取代
|